週期函數,週期波形,傅立葉諧波(泛音)
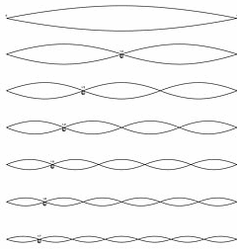
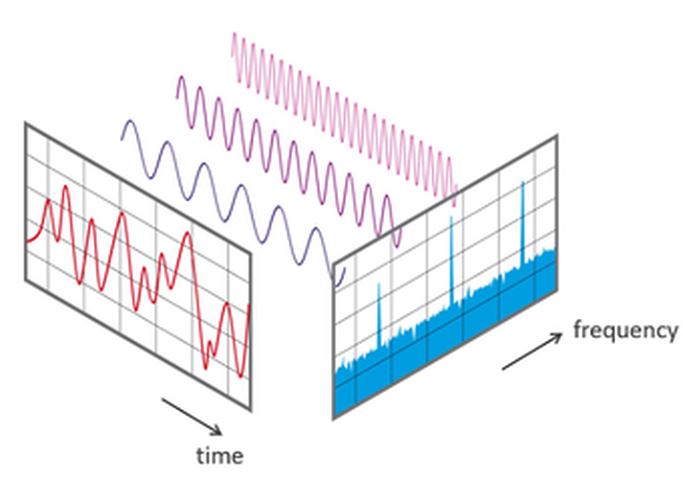
要了解泛音,首先您會聽到琴弦的主要振動,在下面的圖片中,它顯示了涉及整個琴弦長度的振動。接下來,您會聽到一半弦長的振動。它是主要聲音的下一個“八度”。然後,您會聽到由弦長的1 / 3、1 / 4、1 / 5等引起的振動,主聲音中的這些“附加”稱為泛音,有些泛音較大,而另一些則較安靜。這就是每種樂器發出其獨特聲音的原因。
要了解泛音,首先您會聽到琴弦的主要振動,在下面的圖片中,它顯示了涉及整個琴弦長度的振動。接下來,您會聽到一半弦長的振動。它是主要聲音的下一個“八度”。然後,您會聽到由弦長的1 / 3、1 / 4、1 / 5等引起的振動,主聲音中的這些“附加”稱為泛音,有些泛音較大,而另一些則較安靜。這就是每種樂器發出其獨特聲音的原因。
泛音不僅可以在音樂中使用,他們可以為任何循環過程添加有意義的東西,看看軟件計算出的純正弦波與帶有泛音的同一波-豐富波之間的區別。
這是一個145天的波:
這是一個145天的波:
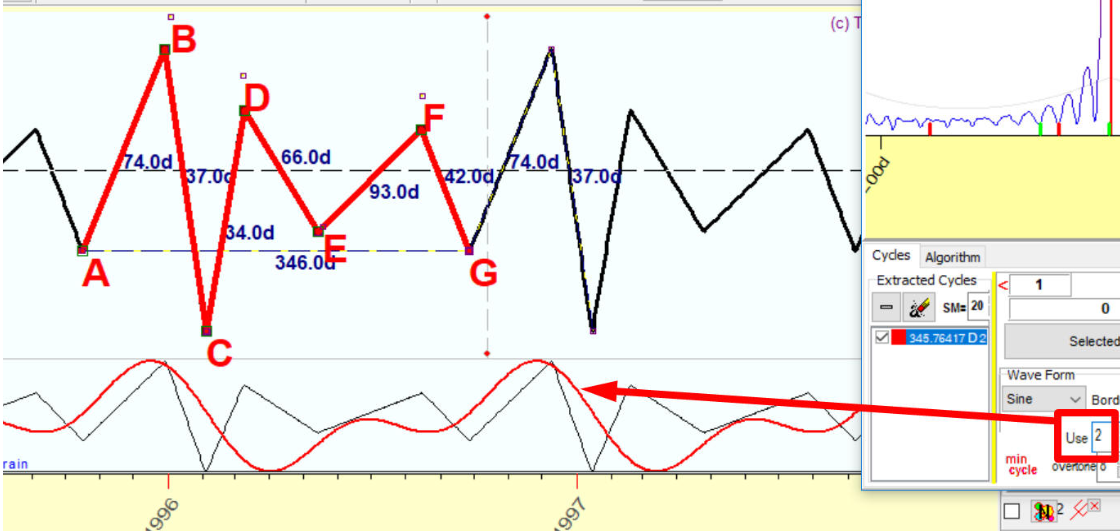
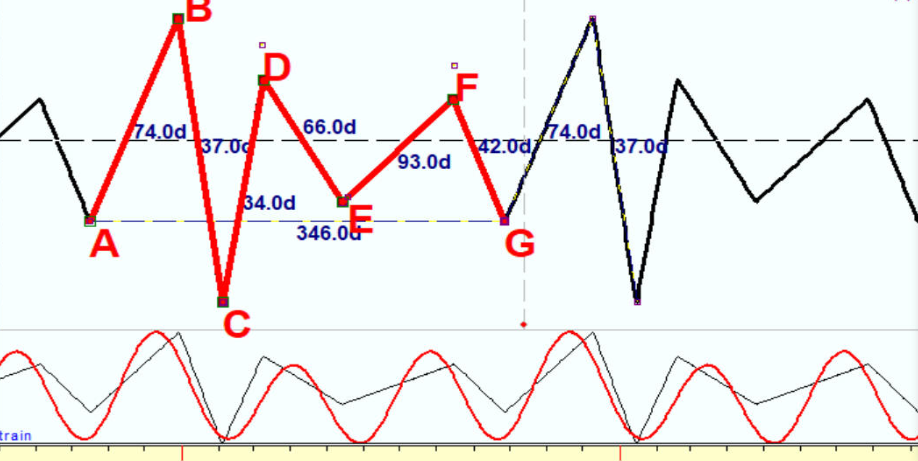
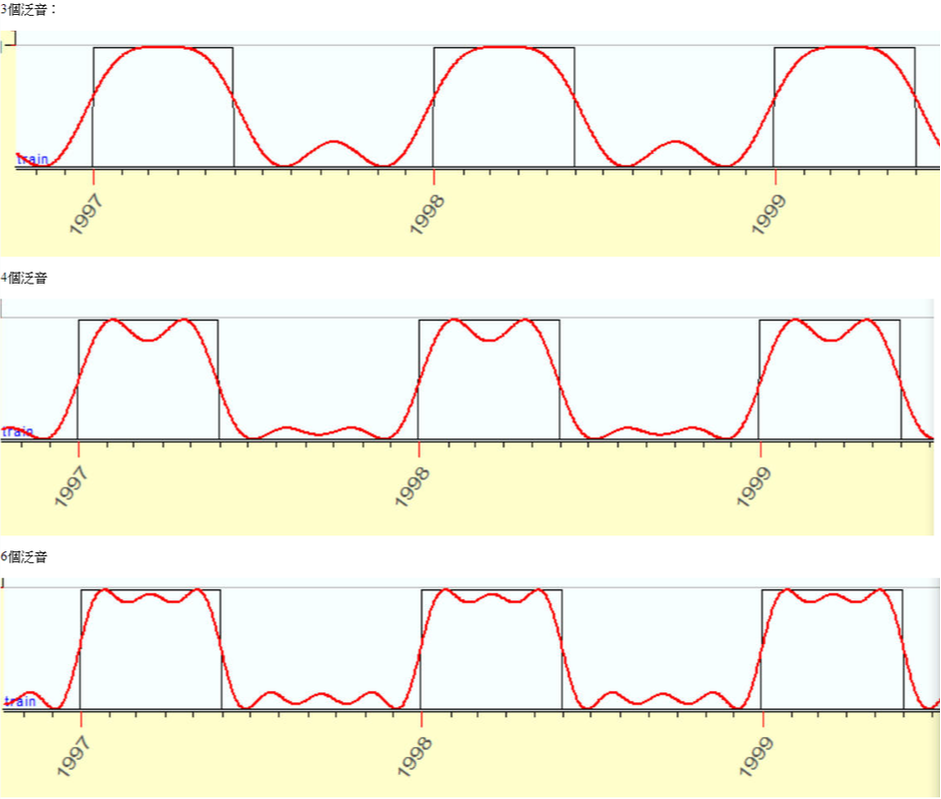
下面是具有兩個泛音和八個泛音的同一波:
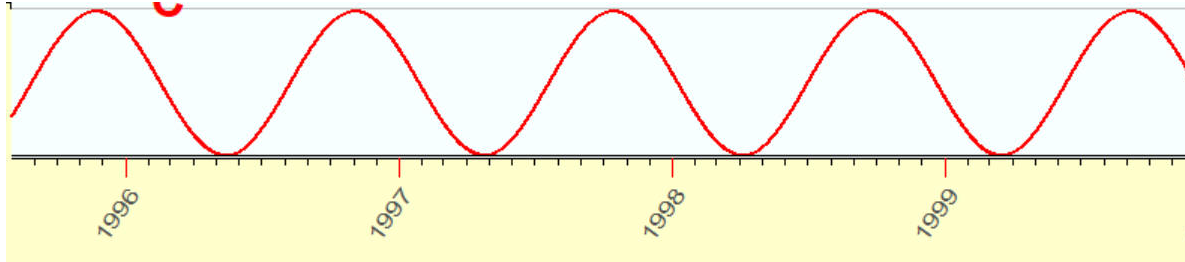
人們經常將周期理解為類似於以下內容的理想性波動:
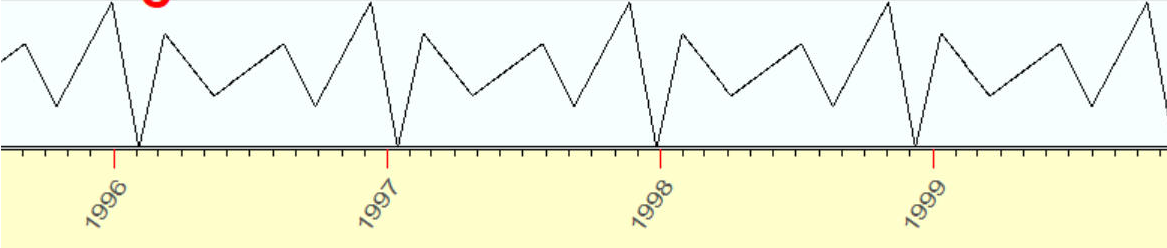
波浪可能看起來像隨機,但其實是有序的循環:
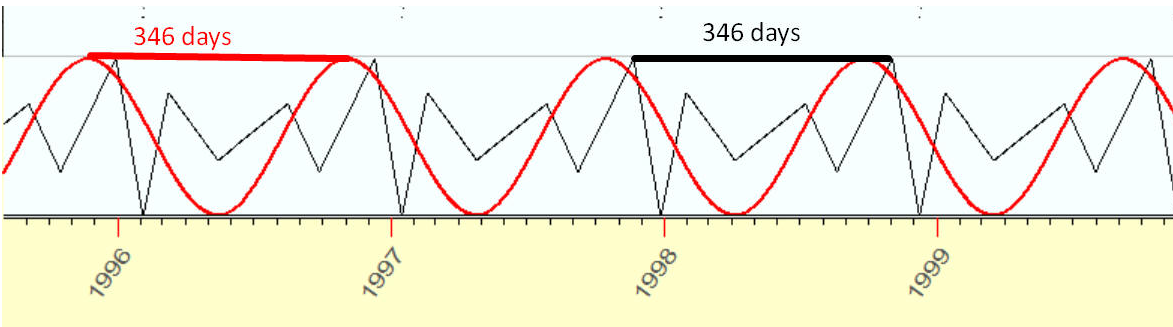
這兩條曲線(即理想的正弦波和上方的不規則波)具有相同的特徵:如果我們在346天上移動任意一條曲線,我們將得到完全相同的曲線。
這兩條曲線(即理想的正弦波和上方的不規則波)具有相同的特徵:如果我們在346天上移動任意一條曲線,我們將得到完全相同的曲線。
這是一個週期這個週期,而這些曲線被稱為 週期函數。這兩條曲線代表不同周期的波形,但周期相同 。
本文的重點是:分析這些不規則波,您無需在此處應用其他數學技術。使用與不規則波動波相同的數學程序分析任何理想的波。
這種方法的數學基礎是 傅里葉系列 技術。對於我們的346天波動的情況,它可能是這樣形成的:週期為346天的任何週期波動都是作為正弦和余弦諧波(或泛音)之和計算的。對於346天,即346天波動,泛音是346/2 = 173天波動,346/3 = 115.3天波動,346/4 = 86.5天波動等。這是公式:
A0 + A1 *(346 d正弦波)+ A2 *(346 d餘弦波)+ A3 *(173 d正弦波)+ A4 *(173 d餘弦波)+ ...
現在,我想演示該技術如何與軟件一起使用。
我已使用以下定期模式手動創建了價格歷史數據集:
本文的重點是:分析這些不規則波,您無需在此處應用其他數學技術。使用與不規則波動波相同的數學程序分析任何理想的波。
這種方法的數學基礎是 傅里葉系列 技術。對於我們的346天波動的情況,它可能是這樣形成的:週期為346天的任何週期波動都是作為正弦和余弦諧波(或泛音)之和計算的。對於346天,即346天波動,泛音是346/2 = 173天波動,346/3 = 115.3天波動,346/4 = 86.5天波動等。這是公式:
A0 + A1 *(346 d正弦波)+ A2 *(346 d餘弦波)+ A3 *(173 d正弦波)+ A4 *(173 d餘弦波)+ ...
現在,我想演示該技術如何與軟件一起使用。
我已使用以下定期模式手動創建了價格歷史數據集:
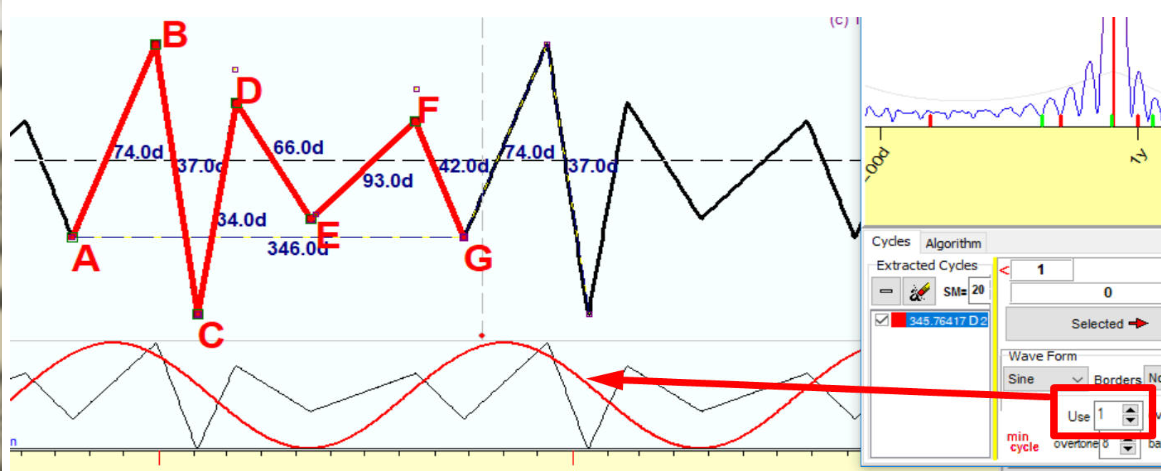
在底部A之後的74天內,我們獲得頂部B;然後在37天之後,我們擁有底部C,在頂部D中擁有34天,在底部E中擁有66天,在頂部F中擁有93天,在底部G中擁有42天。總共,此模式涵蓋346天;每346天重複一次。
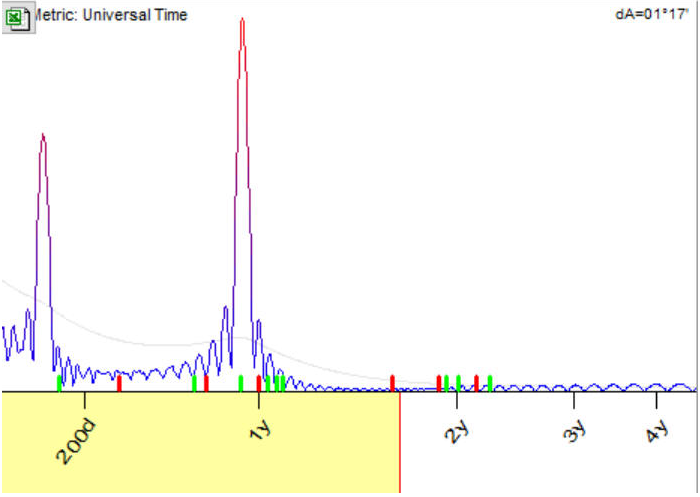
我運行頻譜模塊,立即顯示出存在346天的周期,您會看到那裡的頂峰:
我運行頻譜模塊,立即顯示出存在346天的周期,您會看到那裡的頂峰:
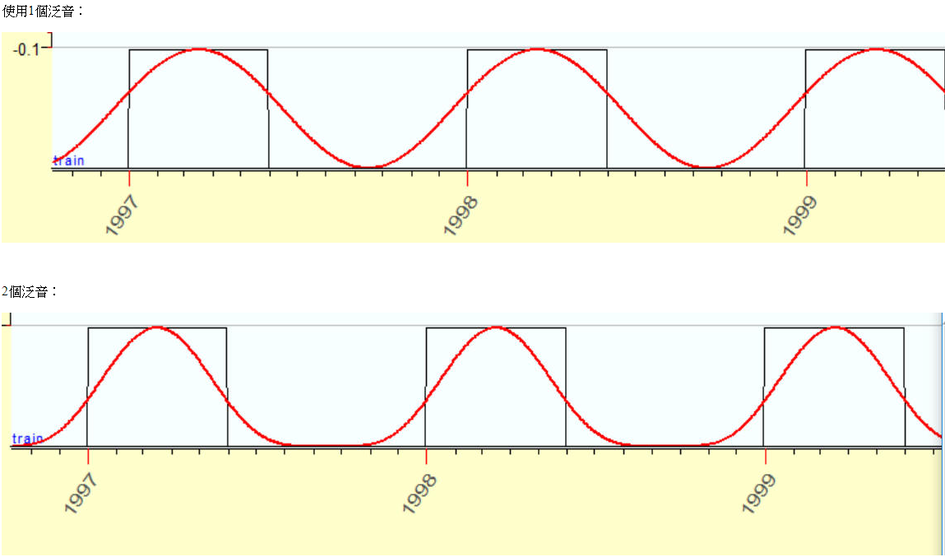
現在我們已經掌握了346天的周期,並要求程序僅使用一個泛音來構建投影線。
即該投影線被計算為兩個波的疊加:正弦346波和余弦346波。
如下圖:
即該投影線被計算為兩個波的疊加:正弦346波和余弦346波。
如下圖: